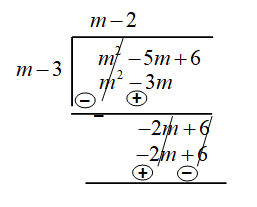Class 8 Model activity Mathematics part 4 2021 | অষ্টম শ্রেণীর নতুন গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট ৪ | ক্লাস এইট মডেল অ্যাক্টিভিটি অংক মডেল অ্যাক্টিভিটি টাস্ক

অষ্টম শ্রেণীর নতুন গণিত মডেল অ্যাক্টিভিটি টাস্ক 2021 পার্ট 4  এর উত্তর নিয়ে আজকের পর্বে আমরা আলোচনা করব। Class 8 Mathematics new model activity task  2021 এর প্রত্যেকটি প্রশ্নের উত্তর সঠিকভাবে আমরা এই পর্বে তোমাদেরকে দেখালাম। আশা করি পূর্বের  মডেল টাস্কের মত এই new Class 7 Model activity task Mathematics 2021 পছন্দ হবে। তাহলে চল শুরু করা যাকঃ 

অষ্টম শ্রেণী গণিত মডেল অ্যাক্টিটভিটি টাস্ক ২০২১

Class 8 Model Activity mathematics task 2021

ক্লাস এইট এর মডেল অ্যাক্টিভিটি টাস্ক 2021 গণিত পার্ট 4

Class 8 model activity task Mathematics 2021 new

 অষ্টম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট 4 2021

গণিত মডেল অ্যাক্টিভিটি টাস্ক 2021

গণিত (Mathematics)

অষ্টম শ্রেণি

---

নীচের প্রশ্নগুলির উত্তর লেখো :

1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQs)

(i)   $\frac{2}{3}$ একটি-

(a) অখণ্ড সংখ্যা  (b) ঋণাত্মক পূর্ণসংখ্যা  (c) মূলদ সংখ্যা  (d) স্বাভাবিক সংখ্যা

উত্তর: (c) মূলদ সংখ্যা 

(ii).   

চিত্রে, আয়তক্ষেত্রাকার জায়গাটির দৈর্ঘ্য এবং প্রস্থের পরিমাপ থেকে ক্ষেত্রফলের পরিমাপে রাশিটির x-এর সহগ হলো -

(a) 2  (b) 1  (c) –6  (d) -3

সমাধানঃ আয়তক্ষেত্রটির ক্ষেত্রফল = (2x² + x)(x-3) বর্গ মিঃ

= 2x³-6x²+x²-3x

=2x³-5x²-3x 

উত্তর: ক্ষেত্রফলের পরিমাপে রাশিটির x-এর সহগ হলো (d) -3

(iii) নীচের প্রতি জোড়া সম্পর্কগুলির মধ্যে সঠিক জোড়া সম্পর্কটি হলো (যেখানে a ও b মূলদ সংখ্যা এবং a ≠ 0; b ≠ 0)

(a) a+b=b+a , a-b=b-a

(b) axb=bxa , a÷b=b÷a

(c) a+b=b+a , a÷b=b÷a

(d) a÷b≠b÷a , a-b≠b-a

উত্তর: (d) a÷b≠b÷a , a-b≠b-a

2. সত্য/মিথ্যা লেখো :

(i) একটি ঘনকের দৈর্ঘ্য y মিটার হলে, উহার আয়তন হবে 3y ঘনমিটার।

উত্তর: উক্তিটি মিথ্যা ।

ব্যাখ্যাঃ একটি ঘনকের দৈর্ঘ্য y মিটার হলে, উহার আয়তন হবে y³ ঘনমিটার।

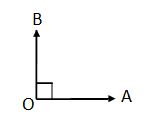
(ii) 

চিত্রে, $OA\bot OB$ এবং কোন ∠ AOB-কে সমদ্বিখণ্ডিত করলে যে দুটি কোণ উৎপন্ন হয় তারা পরস্পরের পূরক কোণ।

উত্তর: উক্তিটি সত্য ।

ব্যাখ্যাঃ যেহেতু $OA\bot OB$ তাই ∠ AOB = 90° তাই সমদ্বিখণ্ডিত করলে যে দুটি কোণ উৎপন্ন হয় তাদের সমষ্টি 90° ।

(iii) একটি সরলরেখার বাইরের কোনো বিন্দু দিয়ে ওই সরলরেখার সমান্তরাল অসংখ্য সরলরেখা আঁকা যায়।

উত্তর: উক্তিটি মিথ্যা ।

আরও পড়ঃ  |  অষ্টম শ্রেনি গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট 1 | Class 8 mathematics model activity task answer part 1

3. ক্লাসের ছাত্রছাত্রীরা কোন কোন খেলা কতজন করে পছন্দ করে শতকরায় তার তালিকা হলো ( একজন কেবলমাত্র একটি খেলাই পছন্দ করবে )

পাই চিত্রে, যে বৃত্তকলাগুলি তথ্যটির অংশগুলিকে বোঝাবে সেই বৃত্তকলাগুলির কেন্দ্রীয় কোণগুলি নির্ণয়  করো এবং তথ্যটির পাই চিত্র অঙ্কন করো ।

সমাধানঃ

পাইচিত্রের মোট কেন্দ্রীয় কোণ 360°

ক্রিকেট নির্দেশক বৃত্তকলার কেন্দ্রীয় কোণ $=360\times \frac{60}{60+30+10}$ °

= $36\not{0}\times \frac{6\not{0}}{1\not{0}\not{0}}$ ° = 216°

ফুটবল নির্দেশক বৃত্তকলার কেন্দ্রীয় কোণ $=36\not{0}\times \frac{3\not{0}}{1\not{0}\not{0}}$ ° = 108°

ব্যাডমিন্টন নির্দেশক বৃত্তকলার কেন্দ্রীয় কোণ $=36\not{0}\times \frac{1\not{0}}{1\not{0}\not{0}}$ ° = 36°

 আরও পড়ঃ  |  অষ্টম শ্রেনি গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট 2 | Class 8 mathematics model activity task answer part 2

 4. (i) $\frac{x}{2}=\frac{1}{2x}+1$ হলে, ${{x}^{3}}-\frac{1}{{{x}^{3}}}$ -এর মান নির্ণয় করো।

সমাধান: $\frac{x}{2}=\frac{1}{2x}+1$

বা, $x=\frac{1}{x}+2$

বা, $x-\frac{1}{x}=2$

এখন , ${{x}^{3}}-\frac{1}{{{x}^{3}}}$

= $\left( x-\frac{1}{x} \right)\left\{ {{x}^{2}}+x.\frac{1}{x}+{{\left( \frac{1}{x} \right)}^{2}} \right\}$

=  $\left( x-\frac{1}{x} \right)\left\{ {{x}^{2}}-2\not{x}.\frac{1}{{\not{x}}}+{{\left( \frac{1}{x} \right)}^{2}}+3\not{x}.\frac{1}{{\not{x}}} \right\}$

= $\left( x-\frac{1}{x} \right)\left\{ {{\left( x-\frac{1}{x} \right)}^{2}}+3 \right\}$

= $2\times ({{2}^{2}}+3)$

= $2\times (4+3)=2\times 7=14$

(ii) ভাগ করো $\left( {{m}^{2}}-5m+6 \right)$  -কে (m - 3) দিয়ে

উত্তর: নির্ণেয় ভাগফল (m-2) ।

আরও পড়ঃ  |  অষ্টম শ্রেনি গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট 3 | Class 8 mathematics model activity task answer part 3