নবম শ্রেণী ভৌত বিজ্ঞান বল ও গতি অনুশীলনী প্রশ্ন উত্তর । class 9 physical science chapter 2 force and motion question answer

 নবম শ্রেণির ভৌতবিজ্ঞান দ্বিতীয় অধায় বল ও গতি - অনুশীলনী প্রশ্ন উত্তর - নিয়ে আজকের পর্বে আলোচনা করব। 

বিভাগ - "ক" বহুবিকল্পভিত্তিক প্রশ্ন (MCQ) - মান 1

1. এক ব্যক্তি 7m ব্যাসার্ধের একটি অর্ধবৃত্তাকার মাঠের পরিধি বরাবর ব্যাসের অপর প্রান্তে গেল। ব্যক্তির সরণ হল -

(A) 14m (B) 16m (C) 22m (D) 25m 

উত্তরঃ (A) 14m

ব্যাখ্যা: পরিধি বরাবর গেলে অতিক্রান্ত দূরত্ব অর্ধ বৃত্তের পরিধি এর সমান হলেও সরণ মাপা হয় শুরু ও শেষ এর বিন্দুদ্বয়ের মাঝের সোজাসুজি দূরত্ব দিয়ে তাই ব্যক্তির সরণ হবে বৃত্তের ব্যাস এর সমান অর্থাৎ 14 মিটার

2. একটি বস্তুকণার প্রাথমিক বেগ 10m/s ও মন্দন 2m/s2। কণাটি কতক্ষণ পরে থামবে?

(A) 2s (B) 4s (C) 5s (D) 6s

উত্তরঃ (C) 5s

3.500g ভরের কোনো বস্তুর ওপর কত বল প্রযুক্ত হলে 2m/s2 ত্বরণ উৎপন্ন হবে?

(A) 1N (B) 1.5N (C) 2N (D) 4N

উত্তরঃ (A) 1N

4. মোটরচালিত একটি বেল্ট 5m/s সমবেগে গতিশীল। যদি ওপর থেকে 1kg/s হারে বালি বেল্টের ওপর ফেলা হয়, তাহলে সমগতি বজায় রাখার জন্য মোটর কত বল প্রয়োগ করবে?

(A) 2.5N (B) 5N (C) 7.5N (D) 10N

উত্তরঃ (B) 5N

5. কোনো বলের দুটি সমকৌণিক উপাংশ 3N ও 4N হলে বলের মান হল

(A) 7N (B) 6N (C) 8N (D) 5N

উত্তরঃ (D) 5N

6. একটি রকেট প্রতি সেকেন্ডে 10kg জ্বালানি দহন করে এবং উৎপন্ন গ্যাস 1000m/s বেগে রকেট থেকে নির্গত হয়। রকেটের ওপর ঊর্ধ্বঘাত হল -

(A) 10000N (B) 5000N (C) 50000N (D)100000N

উত্তরঃ (A) 10000N

7. 4kg ভরবিশিষ্ট একটি বন্দুক থেকে 500m/s বেগে 6g ভরের গুলি ছুড়লে বন্দুকটির প্রতিক্ষেপ বেগ হবে -

(A) 50cm/s (B) 25cm / s (C) 20cm/s (D) 75cm/s

উত্তরঃ - (D) 75cm/s

৪. নীচের চিত্রে একটি কণার বেগ-সময় লেখচিত্র দেখানো হয়েছে। কণার গড় গতিবেগ হল -

(A) 4m/s (B) 6m/s (C) 3m/s (D) 2m/s 

উত্তরঃ - (D) 2m/s 

9. রকেটের গতি যে সংরক্ষণ নীতির ওপর প্রতিষ্ঠিত তা হল-

(A) রৈখিক ভরবেগ (B) বল (C) ভর (D) গতিশক্তি

উত্তরঃ - (A) রৈখিক ভরবেগ

10. কত বল প্রয়োগ করলে 10g ভরের কোনো বস্তুর ত্বরণ 6cm/s2 হবে?

(A) 50 dyn (B) 60 dyn (C) 70 dyn (D) 80 dyn

উত্তরঃ - (B) 60 dyn

11. 1 dyn বল 1 mg ভরের বস্তুর ওপর কাজ করলে কী পরিমাণ ত্বরণ সৃষ্টি হবে?

(A) 5 m/s2 (B) 10m /s2 (C) 15m/s2 (D) 20m/s2

উত্তরঃ - (B) 10m /s2

12. টেবিলের ওপর তোমার একটি বই স্থির অবস্থায় সাম্য বজায় রেখেছে, কারণ

(A) বইটির ওপর সমান মানের ক্রিয়া ও প্রতিক্রিয়া কাজ করছে

(B) বইটির ওপর টেবিল প্রতিক্রিয়া বল প্রয়োগ করছে 

(C) বইটির ওপর ক্রিয়াশীল সমস্ত প্রকার বলের লব্ধি শূন্য

(D) কোনোটিই নয়

উত্তরঃ - (C) বইটির ওপর ক্রিয়াশীল সমস্ত প্রকার বলের লব্ধি শূন্য

13. কোনো বস্তুর ওপর স্থির মানের বল প্রয়োগ করতে থাকলে বস্তুটির -

(A) সমবেগ থাকবে

(B) সমান ভরবেগ থাকবে

(C) সমত্বরণ থাকবে

(D) সমদ্ৰুতি থাকবে

উত্তরঃ - (C) সমত্বরণ থাকবে

14. বলের অধীনে গতিশীল একটি বস্তুর ওপর থেকে কোনো মুহূর্তে বল সরিয়ে নিলে বস্তুটি

(A) ত্বরণসহ চলতে থাকবে

(B) সমবেগে চলতে থাকবে

(C) থেমে যাবে

(D) কোনোটিই নয়

উত্তরঃ - (A) সমবেগ থাকবে

15. চলন্ত গাড়ি হঠাৎ থেমে গেলে আরোহীরা সামনের দিকে হেলে পড়ে, এর কারণ হল

(A) স্থিতিজাড্য

(B) গতিজাড্য

(C) ঘূর্ণন গতি

(D) আপেক্ষিক গতি 

উত্তরঃ - (B) গতিজাড্য

আরও পড়ুনঃ নবম শ্রেণী জীবন বিজ্ঞান দ্বিতীয় অধ্যায় - জীবন সংগঠনের স্তর এর প্রশ্ন উত্তর

আরও পড়ুনঃ পৃষ্ঠটান কাকে বলে | পৃষ্ঠটানের একক মাত্রা উদাহরণ | পৃষ্ঠ শক্তি । নবম শ্রেণী ভৌত বিজ্ঞান প্রশ্ন উত্তর

Mock test দাও: ক্লাস নাইন চ্যাপ্টার: অ্যাসিড (Acid) – Mock Test

বিভাগ "খ" অভিসংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন মান 1

একটি শব্দ বা একটি বাক্যে উত্তর দাও।

1. স্থিতি কাকে বলে?

উত্তরঃ - সময়ের সঙ্গে যে সমস্ত বস্তুর অবস্থানের কোনো পরিবর্তন হয় না, সেই বস্তুকে স্থির বস্তু বলে। বস্তুর এই ধর্মকে স্থিতি বা Rest বলে।

2. গতি কাকে বলে?

উত্তরঃ - সময়ের সঙ্গে যে সমস্ত বস্তুর অবস্থানের পরিবর্তন হয় , সেই সমস্ত বস্তুকে গতিশীল বস্তু বলে। বস্তুর এই ধর্মকে গতিশীলতা বা গতি বলে।

3. ঘূর্ণন গতিতে কী অপরিবর্তিত থাকে?

উত্তরঃ - ঘূর্ণন গতিতে বস্তুর নিজের অক্ষের সাপেক্ষে  অবস্থান অপরিবর্তিত থাকে।

4. বৃত্তপথে গতিশীল কোনো বস্তুর কোনো এক মুহূর্তে বেগের অভিমুখ কোন্ দিক বরাবর হয়? 

উত্তরঃ - বৃত্তাকার পথে গতিশীল কোনো বস্তুর বেগের অভিমুখ হলো ওই বস্তুটি গতিপথের যে বিন্দুতে আছে, সেই বিন্দুতে অঙ্কিত স্পর্শক (tangent) এর দিক বরাবর।

5. সমবৃত্তীয় গতি কাকে বলে?

উত্তরঃ - বৃত্তাকার গতির ক্ষেত্রে দ্রুতি সুষম থাকে তাকে সমবৃত্তীয় গতি বলে। 

6. বেগ-সময় লেখচিত্রের নতি কী নির্দেশ করে?

উত্তরঃ - বেগ-সময় লেখচিত্রের নতি ত্বরণ নির্দেশ করে ।

7. বলের প্রকৃতিগত সংজ্ঞা নিউটনের কোন্ গতিসূত্র থেকে পাওয়া যায়?

উত্তরঃ - বলের প্রকৃতিগত সংজ্ঞা নিউটনের প্রথম গতিসূত্র থেকে পাওয়া যায়।

৪. বলের পরিমাণবাচক সংজ্ঞা নিউটনের কোন্ গতিসূত্র থেকে পাওয়া যায় ?

উত্তরঃ -  বলের পরিমাণবাচক সংজ্ঞা নিউটনের দ্বিতীয় গতি সূত্র থেকে পাওয়া যায়।

9. বলের CGS পদ্ধতি ও SI-তে পরম এককের সম্পর্ক কী?

উত্তরঃ - বলের CGS পদ্ধতিতে পরম একক ডাইন এবং   SI-তে নিউটন ।

1 নিউটন = 10^5 ডাইন।

10. বলের বিভাজন কাকে বলে?

উত্তরঃ - একটি বলকে দুটি অংশে বিভাজিত করার পদ্ধতিকেই  বলের বিভাজন বলে এবং ওই অংশ দুটিকে মূল বলের উপাংশ বলে।

1. স্তম্ভ মেলাও

বাম স্তম্ভ	ডান স্তম্ভ
1. গাছ থেকে একটি ফল সোজা পড়ছে	(A) ঘূর্ণন গতি
2. একটি লাট্টু নির্দিষ্ট স্থানে ঘুরছে	(B) দোলগতি
3. পাথরে সুতো বেঁধে আঙুলের চারপাশে ঘোরানো হচ্ছে	(C) চলন গতি
4. পাথরে সুতো বেঁধে দোলানো হচ্ছে	(D) বৃত্তীয় গতি

উত্তর :

বাম স্তম্ভ	ডান স্তম্ভ
1. গাছ থেকে একটি ফল সোজা পড়ছে	(C) চলন গতি
2. একটি লাট্টু নির্দিষ্ট স্থানে ঘুরছে	(A) ঘূর্ণন গতি
3. পাথরে সুতো বেঁধে আঙুলের চারপাশে ঘোরানো হচ্ছে	(D) বৃত্তীয় গতি
4. পাথরে সুতো বেঁধে দোলানো হচ্ছে	(B) দোলগতি

2. স্তম্ভ মেলাও

বাম স্তম্ভ	ডান স্তম্ভ
1. ভূমির ওপর দাঁড়ানো ব্যক্তির ওপর ভূমি দ্বারা প্রযুক্ত বল সোজা পড়ছে	(A) ঘর্ষণ
2. একটি লোহার টুকরো চুম্বকের দিকে এগিয়ে চলেছে যে বলের প্রভাবে	(B) মহাকর্ষ বল
3. একটি বস্তুকে ভূমির ওপর ঠেলে দিলে সেটি কিছুদূরে গিয়ে থেমে যায় যে বলের জন্য	(C) লম্ব বল
4. পৃথিবী সূর্যের চারপাশে ঘুরে চলেছে যে বলের প্রভাবে	(D) চৌম্বক বল

উত্তর :

বাম স্তম্ভ	ডান স্তম্ভ
1. ভূমির ওপর দাঁড়ানো ব্যক্তির ওপর ভূমি দ্বারা প্রযুক্ত বল সোজা পড়ছে	(A) লম্ব বল
2. একটি লোহার টুকরো চুম্বকের দিকে এগিয়ে চলেছে যে বলের প্রভাবে	(B) বলচৌম্বক বল
3. একটি বস্তুকে ভূমির ওপর ঠেলে দিলে সেটি কিছুদূরে গিয়ে থেমে যায় যে বলের জন্য	(C)ঘর্ষণ
4. পৃথিবী সূর্যের চারপাশে ঘুরে চলেছে যে বলের প্রভাবে	(D)মহাকর্ষ

শূন্যস্থান পূরণ করো।

1. -------- স্থানেও রকেট চলতে পারে।

উত্তরঃ - শূন্য।

2. ক্রিয়া-প্রতিক্রিয়া পরস্পরকে -------- করতে পারে না ।

উত্তরঃ - প্রশমিত।

3. কোনো বস্তুর স্থিতি ও গতি -------- ।

উত্তরঃ - সর্বদা আপেক্ষিক।

4. বিশুদ্ধ ঘূর্ণনের ক্ষেত্রে ঘূর্ণাক্ষ সর্বদাই ----- ।

উত্তরঃ - অপরিবর্তিত । 

5. পৃথিবীর আহ্নিক গতি ---------- গতির উদাহরণ।

উত্তরঃ - ঘূর্ণন।

6. চলন্ত গাড়ি হঠাৎ থেমে গেলে আরোহীরা ------- জন্য ---- দিকে হেলে পড়ে।

 উত্তরঃ - স্থিতি জাড্যের , সামনের।

7. নিউটনের -------- গতিসূত্রকে জাড্যের সূত্র বলা হয়।

উত্তরঃ - জাড্যের সূত্র বা জড়তার সূত্র।

সত্য/মিথ্যা নিরূপণ করো।

1. দ্রুতি শূন্য হলে বেগ শূন্য নাও হতে পারে। 

উত্তরঃ - মিথ্যা।

2. ক্রিয়া ও প্রতিক্রিয়ার যোগফল সর্বদা শূন্য হয়।

উত্তরঃ - সত্য।

3. কোনো বস্তুর ভরবেগের CGS একক g.cm/s 

উত্তরঃ - সত্য।

4. অবাধে পতনশীল বস্তুর গতি হল সমত্বরণযুক্ত গতি।

উত্তরঃ - সত্য।

5. দ্ৰুতি কখনও ঋণাত্মক হয় না।

উত্তরঃ - সত্য।

বিভাগ গ সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন মান 2

1. সব গতি বা স্থিতিই আপেক্ষিক ব্যাখ্যা করো।

উত্তরঃ - 

2. দ্রুতি ও বেগের মধ্যে পার্থক্য লেখো।

উত্তরঃ - 

দ্রুতি	বেগ
1. সচল বস্তু একক সময়ে যে দূরত্ব অতিক্রম করে তাকে ওই বস্তুর দ্রুতি বলে।	1. সচল বস্তুর একক সময়ে সরণকে বস্তুটির বলে।
2. দ্রতি স্কেলার রাশি।	2. বেগ ভেক্টর রাশি।
3. সচল বস্তুর গড় দ্রুতি শূন্য হতে পারে না।	3. সচল বস্তুর গড় বেগ শূন্য হতে পারে।
4. সমদ্রুতি সম্পন্ন বস্তু সমবেগ সম্পন্ন নাও হতে।	4. সমবেগসম্পন্ন বস্তু সমদ্রুতিসম্পন্ন হবেই।
5. বস্তুর গড় দ্রুতি গড় বেগের সমান কিংবা বেশি হয়।	5. বস্তুর গড় বেগ গড় দ্রুতির সমান কিংবা কম হয়।

3. সমবৃত্তীয় গতি বলতে কী বোঝ?

উত্তরঃ - বৃত্তাকার গতির ক্ষেত্রে দ্রুতি সুষম থাকে তাকে সমবৃত্তীয় গতি বলে। অর্থাৎ সমকৌণিক বেগবিশিষ্ট গতিকে সমবৃত্তীয় গতি বলে।

4. বীজগাণিতিক পদ্ধতিতে, v=u+at সমীকরণটি প্রতিষ্ঠা করো। 

উত্তরঃ - মনে করি, কোন গতিশীল বস্তুর-

প্রাথমিক বেগ = u

অতিক্রান্ত সময় = t

অন্তিম বেগ = v

অতএব, বেগের পরিবর্তন = (v-u)

বস্তুর ত্বরণ (a) =

বা, a = 

বা, v-u = at

বা, v = u+at

5. প্রতিমিত বল ও কার্যকর বল বলতে কী বোঝ?

উত্তরঃ - প্রতিমিত বল : কোনো বস্তুর উপর ক্রিয়াশীল একাধিক বলের লব্ধি শূন্য হলে, ওই বলগুলিকে একত্রে প্রতিমিত বল বলে। প্রতিমিত বল এর ক্রিয়ায় বস্তুতে কোন গতি সৃষ্টি হবে না।

কার্যকর বল: কোন বস্তুর উপর ক্রিয়াশীল একাধিক বলের লব্ধি শূন্য না হলে ওই বল গুলির লব্ধি বল কে কার্যকর বল বলে।

6. নিউটনের প্রথম গতিসূত্র থেকে কী কী জানা যায়?

উত্তরঃ - নিউটনের প্রথম গতিসূত্র থেকে (i) বস্তুর জাড্যের বা জড়তার ধারণা ও (ii) বলের সংজ্ঞা।

7. স্থিতিজাড্য কাকে বলে? উদাহরণ দাও। 

উত্তর: যে ধর্মের জন্য স্থির জড়বস্তু তার স্থিতাবস্থা বজায় রাখতে চায় তাকে স্থিতি জাড্য বলে।

৪. গতিজাড্য কাকে বলে? উদাহরণ দাও।

উত্তর: যে ধর্মের জন্য গতিশীল বস্তু সমবেগে সরলরেখায় গতি বজায় রাখার চেষ্টা করে তাকে গতিজাড্য বলে।

9. ভরই বস্তুর জাড্যের পরিমাপ—ব্যাখ্যা করো।

উত্তর: কোনো স্থির বস্তুর স্থির কিংবা গতিশীল বস্তুর গতিশীলতা কার প্রবণতায় হলো বস্তুর জাড্যে বা জড়তা। যে বস্তুর ভর যত বেশি তার জাড্য তত বেশি। অর্থাৎ, কোনো হালকা বস্তুর তুলনায় ভারী বস্তুর অবস্থানের পরিবর্তন করতে বেশী বল প্রয়োগ করতে হয়। তাই কোনো জড় বস্তুর ভরই বস্তুর জাড্যের পরিমাপ।

10. জড়ত্বীয় ভর বলতে কী বোঝ? 

বস্তুর ভর তাদের স্থিতি ও গতি জাড্যের মান নির্দেশ করে। এই কারণে এই ভরকে জড় ভর বা জড়ত্বীয় ভর ( inertial mass )।

স্পষ্টত F = ma সমীকরণে বস্তুর যে ভর নির্দেশ করা হয়েছে তা হলো জড়ত্বীয় ভর ।

11. নিউটন (N) ও ডাইনের (dyn) সম্পর্ক স্থাপন করো। 

উত্তর: 1 নিউটন 

= 1 কিগ্রা × 1 মিটার/ সেকেন্ড²

= 1000 গ্রাম × 100 সেমি / সেকেন্ড²

= 100000 ডাইন

= 10⁵  ডাইন

অর্থাৎ, 1 নিউটন = 10⁵ ডাইন

12. বলের সংযোজন সংক্রান্ত সামান্তরিক সূত্র বিবৃত করো।

উত্তর:

বলের সংযোজন সংক্রান্ত সামান্তরিক সূত্র: 

যদি কোন বিন্দুতে ক্রিয়াশীল দুটি বলকে কোনো সামান্তরিকের দুটি সন্নিহিত বাহু দ্বারা মানে ও অভিমুখে প্রকাশ করা যায় তবে ওই বিন্দু থেকে অঙ্কিত সামান্তরিকের কর্ণটি বলদ্বয়ের লব্ধিকে মানে ও অভিমুখে প্রকাশ করবে।

13. পাখি কীভাবে আকাশে ওড়ে ব্যাখ্যা করো।

উত্তর: একটি পাখি যখন OC অভিমুখে উড়ে যেতে চায় তখন সে তার দুটি ডানা দিয়ে বায়ুর ওপর OA এবং OB অভিমুখে বল প্রয়োগ করে। একই সঙ্গে বায়ুও OE এবং OD অভিমুখে পাখিটির ওপর প্রতিক্রিয়া বল প্রয়োগ করে। এই প্রতিক্রিয়া বলদুটি যেহেতু পাখিটির ওপর প্রযুক্ত হচ্ছে, তাই এই বলদুটিই পাখির গতি সৃষ্টি করে। পাখিটি দুটি ডানা দিয়ে সমান বল প্রয়োগ করলে OC দিকটিই হয় লব্ধি প্রতিক্রিয়ার দিক। কাজেই পাখিটি OC অভিমুখে উড়ে যেতে পারে।

 পাখিটি যখন একটি ডানা দিয়ে অপর ডানার তুলনায় কম বল প্রয়োগ করে তখন লব্ধি প্রতিক্রিয়া আর OC অভিমুখে ক্রিয়া করে না, যেদিকে কম বল প্রযুক্ত হয় সেদিকে কিছুটা হেলে যায়। অর্থাৎ পাখিটির গতির দিক পরিবর্তিত হয়। স্পষ্টতই বায়ুশূন্য স্থানে পাখি প্রয়োজনীয় প্রতিক্রিয়া বল পায় না বলেই উড়তে পারে না।

14. কামান থেকে গোলা ছুড়লে কামান পিছু হঠে কেন? 

উত্তর: যখন কোন কামান থেকে গোলা ছোড়া হয় তখন গলার ওপর একটি বল ক্রিয়া করে ফলে গোলাটি সামনের দিকে এগিয়ে যায়। গোলা কামানের ওপর সমান ও বিপরীতমুখী প্রতিক্রিয়া বল প্রয়োগ করে। ফলে কামানটি ও পিছন দিকে সরে যায়। তৃতীয় গতিসূত্রের সাহায্যে এর ব্যাখ্যা করা যায়।

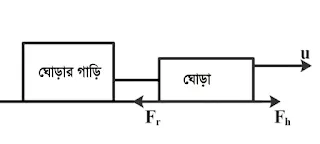
15. ঘোড়া গাড়িকে যে বলে টানে গাড়িও ঘোড়াকে সমান বলে বিপরীত দিকে টানে। তাহলে গাড়ি চলে কী করে?

উত্তর:

চিত্রে দেখানো হয়েছে, ঘোড়ার গতির দিকটি সামনের দিকে। আমরা জানি যে প্রতিক্রিয়া বল সবসময় জোড়ায় থাকে। সুতরাং, চিত্রে দেখানো হিসাবে, ঘোড়াটি যদি দেখানো হিসাবে পিছনের দিকে একটি বল প্রয়োগ করে, তাহলে ঘোড়াটির উপর ভূমি দ্বারা প্রয়োগ করা একটি প্রতিক্রিয়া বল থাকবে সমান মাত্রায় কিন্তু দিক বিপরীত দিকে। এই বল ঘোড়াকে সামনের দিকে যেতে সাহায্য করে। ঘোড়া এগিয়ে যাওয়ার সাথে সাথে বলটি গাড়িটিকে টানতে থাকে।

সুতরাং, ঘোড়ার নড়াচড়া মাটি দ্বারা প্রয়োগ করা বলের কারণে হয়। এই বল ঘর্ষণ বল নামে পরিচিত।ঘর্ষণ একটি প্রতিক্রিয়া বল। ঘর্ষণ বল সবসময় বস্তুর গতির দিকের বিপরীতে কাজ করে।

বিভাগ ঘ দীর্ঘ উত্তরভিত্তিক প্রশ্ন

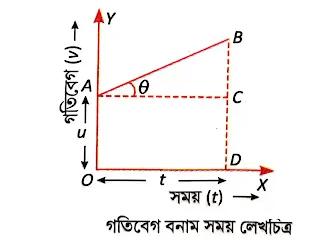
1. লেখচিত্রের সাহায্যে s =$\frac{1}{2}a{{t}^{2}}$ সমীকরণটি প্রতিষ্ঠা করো ।

উত্তর: উত্তর: আমরা জানি, কোন নির্দিষ্ট সময় অবকাশে বস্তুর বেগ-সময় লেখচিত্রের ক্ষেত্রফল ওই অবকাশে বস্তুর অতিক্রান্ত দূরত্ব নির্দেশ করে।

∴ t সময়ে বস্তুটির অতিক্রান্ত দূরত্ব (s) = চিত্রে অঙ্কিত ACB ত্রিভুজের ক্ষেত্রফল ।

চিত্র অনুযায়ী , ত্বরণ (a) = বেগ বৃদ্ধি ÷ সময় = $\frac{BC}{OD}=\frac{BC}{AC}$

S = ACB ত্রিভুজের ক্ষেত্রফল

= $\frac{1}{2}$×AC×BC

=$\frac{1}{2}$×AC× (a×AC)  [$a=\frac{BC}{AC}$]

= $\frac{1}{2}$× t (a×t)

=  $\frac{1}{2}a{{t}^{2}}$

∴ s = $\frac{1}{2}a{{t}^{2}}$ [ প্রমাণিত ]

2.লেখচিত্রের সাহায্যে, s = ut+$\frac{1}{2}a{{t}^{2}}$ সমীকরণটি প্রতিষ্ঠা করো।

উত্তর: আমরা জানি, কোন নির্দিষ্ট সময় অবকাশে বস্তুর বেগ-সময় লেখচিত্রের ক্ষেত্রফল ওই অবকাশে বস্তুর অতিক্রান্ত দূরত্ব নির্দেশ করে।

∴ t সময়ে বস্তুটির অতিক্রান্ত দূরত্ব (s) = চিত্রে অঙ্কিত AODB ট্রাপিজিয়ামের ক্ষেত্রফল।

চিত্র অনুযায়ী , ত্বরণ (a) = বেগ বৃদ্ধি ÷ সময় = $\frac{BC}{OD}=\frac{BC}{AC}$

S = AODB ট্রাপিজিয়ামের ক্ষেত্রফল

= AODC আয়তক্ষেত্রের ক্ষেত্রফল + ACB ত্রিভুজের ক্ষেত্রফল

= OA× OD +$\frac{1}{2}$×AC×BC

= OA× OD +$\frac{1}{2}$×AC× (a×AC)  [$a=\frac{BC}{AC}$]

= ut + $\frac{1}{2}$× t (a×t)

= ut + $\frac{1}{2}a{{t}^{2}}$

∴ s = ut + $\frac{1}{2}a{{t}^{2}}$ [ প্রমাণিত ]

3. লেখচিত্রের সাহায্যে v2 = u2+2as সমীকরণটি প্রতিষ্ঠা করো।

উত্তর: চিত্রে AODB ট্রাপিজিয়ামের ক্ষেত্রফল

= $\frac{1}{2}$×OD×(OA+BD)

বা, s = $\frac{1}{2}$ ×AC×(OA+BD)

= $\frac{1}{2}\times \frac{BC}{a}\times (OA+BD)$

= $\frac{1}{2}\times \frac{(BD-CD)(OA+BD)}{a}$

= $\frac{(BD-OA)(B+OA)}{2a}$

= $\frac{(v-u)(v+u)}{2a}$

= ${{v}^{2}}-{{u}^{2}}=2as$

= ${{v}^{2}}={{u}^{2}}+2as$ [প্রমাণিত]

4. একটি কণার প্রাথমিক বেগ 5m/s। 2s, 4s, 6s ও 10s সময়ে বেগ যথাক্রমে 9m/s, 13m/s, 17m/s ও 25m/s হলে, বেগ-সময় লেখচিত্র অঙ্কন করো।

 

5. নিউটনের দ্বিতীয় গতিসূত্রের সাহায্যে F = ma সমীকরণটি প্রতিষ্ঠা করো।

উত্তরঃ ধরি m ভরের একটি বস্তুর উপর t সময় ধরে F পরিমাণ বল প্রয়গ করায় বস্তুটির বেগ u থেকে বেড়ে v হল।

বস্তুটির প্রাথমিক ভরবেগ = mu

বস্তুটির অন্তিম ভরবেগ =mv

ভরবেগের পরিবর্তন = mv-mu

ভরবেগের পরিবর্তনের হার = $\frac{mv-mu}{t}$

= $\frac{m(v-u)}{t}$

= ma    [ কারণ, $\frac{(v-u)}{t}=a$]

নিউটনের দ্বিতীয় গতিসুত্র অনুযায়ী , $F\propto ma$

বা, $F=k.ma$[ k হল ভেদধ্রুবক । এর মান 1 ]

বা, F=ma

6. একটি বায়ুপূর্ণ বেলুনের মুখ খোলা অবস্থায় নীচের দিকে রাখলে বেলুনটি ওপরের দিকে উঠে যায় কেন? 

একটি বায়ু পূর্ণ বেলুনের মুখ খোলা অবস্থায় নিচের দিকে রাখলে বেলুন থেকে উচ্চচাপের ওই বায়ু বেলুনের সরু মুখ দিয়ে তীব্র বেগে বেরিয়ে আসে। এর ফলে বিপরীতমুখী এক প্রচণ্ড প্রতিক্রিয়া বলের সৃষ্টি হয়। এই প্রতিক্রিয়া বলের জন্য বেলুনটি সামনের দিকে উড়তে থাকে। বেলুন থেকে নির্গত বায়ুর ভরবেগ থাকে। ভরবেগের সংরক্ষণ নীতির জন্যই মিলন বায়ু নির্গমনের বিপরীত দিকে উড়ে চলে।

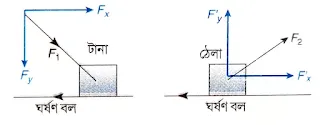
7. বলের সমকৌণিক উপাংশে বিভাজনের সাহায্যে রোলার টানা ও ঠেলা ব্যাখ্যা করো।

বাস্তব দৃষ্টান্ত—কোনো বস্তুকে ঠেলা বা টানা: পেছন দিক থেকে ঠেলে বা সামনের দিক থেকে টেনে কোনো বস্তুকে অনুভূমিক তলে গতিশীল করা যায়। বস্তুটিকে যখন ঠেলা হয় তখন প্রযুক্ত বল F₁ সাধারণত কোণাকুণিভাবে নীচের দিকে ক্রিয়া করে। বস্তুটির অনুভূমিক গতি F₁-এর অনুভূমিক উপাংশ F_x দ্বারা নির্ধারিত হয়। উল্লম্ব উপাংশ F_y নীচের দিকে ক্রিয়া করার ফলে বস্তুটির ওজন কার্যত বৃদ্ধি পায়। তাই বস্তুটিকে ঠেলতে কষ্ট হয়।

অন্যদিকে, বস্তুটিকে যখন টানা হয় তখন প্রযুক্ত বল F₂ সাধারণত কোণাকুণিভাবে ওপরদিকে ক্রিয়া করে। এক্ষেত্রেও F₂-এর অনুভূমিক উপাংশ F'_x-দ্বারা বস্তুর অনুভূমিক গতি নির্ধারিত হয়। এখানে উল্লম্ব উপাংশ F'_y ওপরদিকে ক্রিয়া করার ফলে বস্তুটির ওজন কার্যত হ্রাস পায়। তাই বস্তুটিকে সহজেই টানতে পারা যায়।

সুতরাং কোনো বস্তুকে গতিশীল করতে হলে তাকে ঠেলার চেয়ে টানা সুবিধাজনক।

৪. রৈখিক ভরবেগের সংরক্ষণ নীতিটি লেখো এবং নিউটনের তৃতীয় গতিসূত্রের সাহায্যে প্রমাণ করো।

রৈখিক ভরবেগের সংরক্ষণ সূত্র : কোনো বস্তু সংস্থার উপর বাইরে থেকে কোন বল প্রযুক্ত না হলে বস্তু সংস্থার মোট রৈখিক ভরবেগ (মান ও অভিমুখ) অপরিবর্তিত থাকবে।

দুটি বস্তুর মধ্যে সংঘর্ষের ক্ষেত্রে নিউটনের তৃতীয় গতিসূত্র থেকে রৈখিক ভরবেগের সংরক্ষণ সূত্র প্রমাণ করা যায়। ধরা যাক ${{m}_{1}}$ও ${{m}_{2}}$ ভরের দুটো বস্তু যথাক্রমে ${{u}_{1}}$ও ${{u}_{2}}$গতিবেগে একই রেখা বরাবর একই অভিমুখে গতিশীল থাকাকালীন সংঘাত ঘটায় এবং সংঘাতের পর একই অভিমুখে যথাক্রমে ${{v}_{1}}$ও ${{v}_{2}}$গতিবেগ প্রাপ্ত হয়।

ধরা যাক সংঘাতের সময় বস্তু দুটি খুব অল্পসময়ের (t) জন্য পরস্পরের সংস্পর্শে আসে এবং ${{m}_{1}}$ বস্তুটি ${{m}_{2}}$ বস্তুর উপর ${{F}_{2}}$এবং ${{m}_{2}}$ বস্তুটি ${{m}_{1}}$ বস্তুর উপর ${{F}_{1}}$ বল প্রয়োগ করে।

সুতরাং নিউটনের তৃতীয় গতিসূত্র অনুযায়ী ক্রিয়া ও প্রতিক্রিয়া বল সমান ও বিপরীতমুখী হওয়ায় , ${{F}_{1}}={{F}_{2}}$

এখন ${{F}_{1}}$= ${{m}_{1}}$ ভরের বস্তুর ভরবেগের পরিবর্তনের হার $\frac{{{m}_{1}}{{v}_{1}}-{{m}_{1}}{{u}_{1}}}{t}$

একইভাবে , ${{F}_{2}}$= ${{m}_{2}}$ ভরের বস্তুর ভরবেগের পরিবর্তনের $\frac{{{m}_{2}}{{v}_{2}}-{{m}_{2}}{{u}_{2}}}{t}$
$\therefore $ $\frac{{{m}_{1}}{{v}_{1}}-{{m}_{1}}{{u}_{1}}}{t}$= $-\frac{{{m}_{2}}{{v}_{2}}-{{m}_{2}}{{u}_{2}}}{t}$

বা, ${{m}_{1}}{{v}_{1}}-{{m}_{1}}{{u}_{1}}=-{{m}_{2}}{{v}_{2}}+{{m}_{2}}{{u}_{2}}$

বা, ${{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$

সংঘাতের পূর্বে বস্তুসংস্থান মোট রৈখিক ভরবেগ = সংঘাতের পর বস্তুসংস্থান মোট রৈখিক ভরবেগ।

এটি রৈখিক ভরবেগ সংরক্ষণ সূত্র।

9. একটি মোটরগাড়ি ও একটি লরি একই ভরবেগ নিয়ে চলছিল। সমান বিরুদ্ধ বল প্রয়োগ করে এদের থামানো হলে কোন্‌টি কম সময়ে থামবে নির্ণয় করো।

মোটরগাড়ি ও লরির মধ্যে লরির ভর অনেক বেশি। শেষ পর্যন্ত দুটিকেই থামাতে হবে অর্থাৎ দুটির বেগ শূন্য করতে হবে। অর্থাৎ অন্তিম ভরবেগ মোটরগাড়ি ও লরি উভয়েরই শূন্য করতে হবে। যেহেতু মোটর গাড়ির ভর তুলনামূলকভাবে অনেক কম তাই ভরবেগের পরিবর্তনও কম। নিউটনের দ্বিতীয় গতি সূত্র অনুযায়ী প্রযুক্ত বল ভরবেগের পরিবর্তনের হার এর সমানুপাতিক। তাই সুমান বিরুদ্ধ বলপ্রয়োগ করে থামানো হলে মোটরগাড়ি টি তাড়াতাড়ি কম সময়ে থামবে।

 

বিভাগ ঙ গাণিতিক প্রশ্ন মান 2/3

1. এক ব্যক্তি পূর্বদিক বরাবর 8m যাবার পর দক্ষিণ দিক বরাবর 6m গেল। ব্যক্তির সরণের মান কত?

উত্তরঃ ব্যক্তির সরণের মান = $\sqrt{{{8}^{2}}+{{6}^{2}}}$m 

= $\sqrt{64+36}$m

= $\sqrt{100}$m = 10m

2. একটি কণা সরলরেখা বরাবর সমত্বরণে গতিশীল।

সময় (s)	0	2	4	6	8
বেগ (m/s)	0	6	12	18	24

বিভিন্ন সময়ে কণার বেগের তালিকা থেকে লেখচিত্র তঅঙ্কন করো এবং 3s পরে কণার বেগ নির্ণয় করো।

3. 0.5 kg ভরের কোনো বস্তুর ওপর একটি নির্দিষ্ট বল ক্রিয়া করে 2 m.s^-2 ত্বরণ সৃষ্টি করল। প্রযুক্ত বলের মান নিউটন এককে নির্ণয় করো।

উত্তরঃ আমরা জানি প্রযুক্ত বল = বস্তুর ভর × বস্তুতে উৎপন্ন ত্বরণ

= 0.5×2 নিউটন

= 1 নিউটন

4. 100dyn এর একটি বল 5s ধরে 25g ভরের বস্তুর ওপর ক্রিয়া করল। কত বেগ উৎপন্ন হবে নির্ণয় করো।

উত্তরঃ এক্ষেত্রে F=100 dyn , m = 25g , t = 5s , u = 0

এখন, F=ma সমীকরণ থেকে পাই ,

100 = 25×a

বা, a = $\frac{100}{25}$ =$4cm/{{s}^{2}}$

আবার , v=u+at সমীকরণ থেকে পাই ,

V = 0 + 4×5 cm/s = 20 cm/s

∴ বস্তুতে বেগ উৎপন্ন হবে 20 cm/s

5. 5kg ভরের একটি বস্তু 10m/s বেগে চলছে। একে 20s সময়ে থামাতে কত বল প্রয়োগ করতে হবে?

উত্তরঃ এক্ষেত্রে, m=5kg, u=10m/s , t = 20s , v = 0

বস্তুর মন্দন (a) = $\frac{u-v}{t}$= $\frac{10}{20}m/{{s}^{2}}$= $\frac{1}{2}m/{{s}^{2}}$

এখন, F = ma অনুযায়ী,

প্রযুক্ত বল = $5\times \frac{1}{2}$ dyn = 2.5 dyn

6. চিত্রে একটি কণার বেগ - সময় লেখচিত্র দেখানো হয়েছে।

 

নির্ণয় করো – (i) 10s-এ কণা দ্বারা অতিক্রান্ত দূরত্ব, (ii) সমবেগে গতিশীল অবস্থায় কণার অতিক্রান্ত দূরত্ব।

 

 7. 20g ভরের একটি বস্তুর প্রাথমিক বেগ 10cm/s এবং 5s পরে এর বেগ হল 40cm/s । বস্তুর ওপর ক্রিয়াশীল বলের মান নির্ণয় করো।

উত্তরঃ এক্ষেত্রে ভর (m) = 20g

প্রাথমিক বেগ (u) = 10cm/s

অন্তিম বেগ (v) = 40cm/s

সময় (t) = 5s

আমরা জানি F = ma

বা F = $m.\frac{(v-u)}{t}$ ডাইন

বা, F = $20\times \left( \frac{40-20}{5} \right)$ ডাইন

বা, F = $20\times \frac{20}{5}$ ডাইন

বা , F = 80 ডাইন

8. 5kg ভরের একটি বন্দুক থেকে 20 g ভরের একটি বুলেট 400 m/s বেগে নির্গত হলে বন্দুকের প্রতিক্ষেপ বেগ নির্ণয় করো।

উত্তরঃ গুলির ভর (m) = 20g = 0.002kg , বন্দুকের ভর (M) = 5kg , গুলির বেগ (v)= 400 m/s

গুলি ছোড়ার পর বন্দুকের বেগ v হলে, রৈখিক ভরবেগের সংরক্ষণ সূত্রানুযায়ী,

(M+m)×0 = m×v×M×V

∴ V = $-\frac{mv}{M}$ = $=\frac{0.002\times 400}{5}$m/s = - 0.16v m/s

বন্দুকের প্রতিক্ষেপ বেগ 0.16v m/s