নীচের প্রশ্নগুলির উত্তর লেখ :
1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQ) :
(i) 4pq – এর দুটি সংখ্যামালার অন্তরফল রুপে প্রকাশ হলো
(a) ${{p}^{2}}-{{q}^{2}}$ (b) ${{\left( \frac{p+q}{2} \right)}^{2}}-{{\left( \frac{p-q}{2} \right)}^{2}}$
(c) ${{(p-q)}^{2}}-{{(p+q)}^{2}}$ (d) ${{(p+q)}^{2}}-{{(p-q)}^{2}}$
উত্তর : (d) ${{(p+q)}^{2}}-{{(p-q)}^{2}}$
(ii) গতিবেগ নির্নয়ের সঠিক সম্পর্কটি হলো ( যেখানে প্রয়োজনীয় সময় t , অতিক্রান্ত দূরত্ব d এবং গতিবেগ v )
(a) v=t×d (b) v×d=t
(c) v×t = d (d) v=t+d
উত্তর : (c) v×t = d
(iii) চিত্রে $\angle 1$ ও $\angle 2$পরস্পর
(a) বিপ্রতীপ কোণ (b) একান্তর কোণ
(c) সন্নিহিত কোণ (d) অনুরুপ কোণ
উত্তর : (d) অনুরুপ কোণ
(iv) দৈর্ঘ্যের সমান্তরাল রাস্তার চওড়া 2মি. এবং প্রস্থের সমান্তরাল চউড়া 3মি. । দৈর্ঘ্যের সমান্তরাল রাস্তার ক্ষেত্রফল হলো
(a) 24 বর্গমি. (b) 16 বর্গমি.
(c) 30 বর্গমি. (d) 20 বর্গমি.
উত্তর : (d) 20 বর্গমি.
2. সত্য / মিথ্যা লেখ (T/F) :
(i) পিকটোগ্রাফ অঙ্কনের জন্য দি স্তম্ভ লেখ ব্যাবহার করা হয়।
উত্তর : বিবৃতিটি মিথ্যা ।
(ii) গতিবেগ একই থাকলে সময় ও দূরত্ব সরল সরল সমানুপাতি ।
উত্তর : বিবৃতিটি সত্য।
(iii) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল = $\frac{1}{2}$×ভুমি × উচ্চতা
উত্তর : বিবৃতিটি সত্য।
(iv) $\sqrt{1.21}$= -1.1
উত্তর : বিবৃতিটি সত্য।
ব্যখ্যা : $\sqrt{1.21}=\pm 1.1$
অর্থাৎ , +1.1 × +1.1 = 1.21 আবার -1.1 × -1.1 = 1.21
[ দুটি ঋণাত্বক সংখ্যার গুণফল সর্বদা ধনাত্মক হয়।]
3. সংক্ষিপ্ত উত্তরধর্মি প্রশ্ন :
(i) $\left( 4{{a}^{2}}+4+\frac{1}{{{a}^{2}}} \right)$ বীজগাণিতিক সংখ্যামালাকে পূর্ণবর্গাকারে লেখ ।
সমাধান : $\left( 4{{a}^{2}}+4+\frac{1}{{{a}^{2}}} \right)$
= ${{(2a)}^{2}}+2.2\not{a}.\frac{1}{{\not{a}}}+{{\left( \frac{1}{a} \right)}^{2}}$
= ${{\left( 2a+\frac{1}{a} \right)}^{2}}$
উত্তর : $\left( 4{{a}^{2}}+4+\frac{1}{{{a}^{2}}} \right)$ কে পূর্ণবর্গাকারে প্রকাশ করলে পাই ${{\left( 2a+\frac{1}{a} \right)}^{2}}$
(ii) সমকোণী ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যগুলির মধ্যে সম্পর্ক লেখ।
একটি সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য 5 সেমি. এবং ভুমির দৈর্ঘ্য 3 সেমি. হলে লম্বের দৈর্ঘ্য নির্ণয় কর।
উত্তর : সমকোণী ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যগুলির মধ্যে সম্পর্ক:
লম্ব 2 + ভুমি2 = অতিভুজ2
▣ আমরা জানি , লম্ব2 + ভুমি2 = অতিভুজ2
বা, লম্ব 2 + ভূমি2 = অতিভুজ 2
বা , লম্ব 2+ 9= 25
বা , লম্ব 2= 25-9=16
বা, লম্ব = $\sqrt{16}=4$
উত্তর : ত্রিভুজটির লম্বের দৈর্ঘ্য 4 সেমি.
4. সপ্তম শ্রেনির 34 জন ছাত্রছাত্রীর ও অষ্টম শ্রেনির 40 ছাত্রছাত্রীর প্রিয় খেলার তথ্য নিচের টেবিলে লেখা হয়েছে । এই তথ্য দ্বিস্তম্ভ চিত্রের মাধ্যমে প্রকাশ কর :
| খেলা | ক্রিকেট | ফুটবল | সাঁতার |
|---|---|---|---|
| সপ্তম শ্রেণির ছাত্রছাত্রী | 12 | 14 | 8 |
| অষ্টম শ্রেণির ছাত্রছাত্রী | 14 | 16 | 10 |
উত্তর :
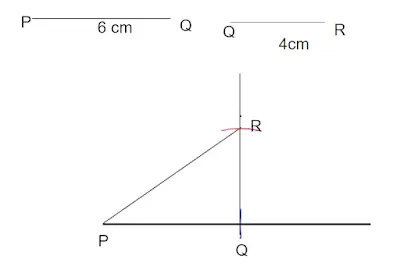
5. PQR একটি সমকোণী ত্রিভুজ আঁক যার $\angle PQR={{90}^{\circ }}$, PQ=6 সেমি. ও QR = 4 সেমি. ।
উত্তর :
অঙ্কন প্রণালি নিচের ভিডিওতে :
অথবা ,
100 মিটার লম্বা একটি ট্রেন ঘণ্টায় 60 কিমি বেগে একটি গাছকে অতিক্রম করতে কত সময় নেবে ?
সমাধান : একটি গাছ অতিক্রম এর অর্থ হলো ট্রেনের নিজের দৈর্ঘ্য অতিক্রম করা ।
60 কিমি = 60 × 1000 মিটার = 60000 মিটার ।
1 ঘণ্টা = 60 × 60 সেকেন্ড = 3600 সেকেন্ড
এখন ,
60000 মিটার অতিক্রম করে 3600 সেকেন্ডে
$\therefore $ 1 ,, ,, ,, $\frac{3600}{60000}$ সেকেন্ডে
$\therefore $ 100 ,, ,, ,, $\frac{36\not{0}\not{0}\times 1\not{0}\not{0}}{6\not{0}\not{0}\not{0}\not{0}}$ সেকেন্ডে
উত্তর : ট্রেনটি গাছটিকে অতিক্রম করতে 6 সেকেন্ড সময় নেবে।